Solving Convex MINLP Problems with AIMMS

Author: Marcel Hunting.

This document describes the Quesada and Grossman algorithm that is implemented in AIMMS to solve convex MINLP problems. We benchmark this algorithm against AOA which implements the classic outer approximation algorithm.

Important

To use this article as reference, please use the whitepaper PDF: Solving-Convex-MINLP-Problems-with-AIMMS.pdf.

Introduction

Convex Mixed Integer Nonlinear Programming (MINLP) problems are MINLP minimization problems in which the objective function and all constraint functions are convex. We assume that the feasible region is convex if the integrality condition is relaxed. Convex MINLP problems can be solved more efficiently than non-convex MINLP problems.

The outer approximation algorithm was introduced by Duran and Grossmann in 1986 [8] to solve convex MINLP problems. The algorithm solves an alternating sequence of nonlinear (NLP) problems and mixed-integer linear (MIP) problems. It was shown that the algorithm finds a global optimum solution in a finite number of steps. Later the outer approximation algorithm was modified by Viswanathan and Grossmann [14] to also handle non-convex MINLP problems but in that case the algorithm cannot guarantee to find a global optimal.

The outer approximation algorithm of Duran and Grossmann was implemented in AIMMS [2] as the AIMMS Outer Approximation (AOA) algorithm. The first version of AOA was introduced in AIMMS 3.3. After the introduction of the GMP library in AIMMS 3.5, the AOA algorithm was rewritten using the GMP functionality; this GMP version of AOA was released in AIMMS 3.6. The GMP version of AOA is described in [10]. In the remainder of this paper we let AOA refer to the GMP version.

AOA by default assumes that the MINLP problem is non-convex and uses an iteration limit as stopping criterion. For AOA the user can flag that the problem is convex in which case AOA will terminate if the objective of the MIP problem becomes larger than the objective of the NLP problem (in case of minimization).

Quesada and Grossmann [12] noticed that the classic outer approximation algorithm often spends a large amount of time in solving the MIP problems in which a significant amount of rework is done. They proposed an algorithm (sometimes called the LP/NLP-Based Branch-and-Bound algorithm) in which only one MIP problem is solved. The Quesada-Grossmann algorithm was implemented in AIMMS 3.9; we use the name COA to refer to the AIMMS implementation. (The “C” in COA stands for “callback”.) Both AOA and COA are “white box” algorithms that allow modifications of the algorithm by the user.

Other solvers available in AIMMS for solving MINLP problems are BARON [13] and KNITRO [5].

We start with a brief description of COA. Next we show how COA and AOA can be used to solve convex MINLP problems. Finally we present results of AOA and COA on problems that are publicly available and often used for benchmarking MINLP solvers.

The COA Algorithm

The main advantage of COA over AOA is that the need of restarting the branch-and-bound tree search is avoided and only a single branch-and-bound tree is required. For a technical review of the Quesada and Grossmann algorithm we refer to [1]. Here we limit ourselves to describing the algorithm as implemented in COA in words:

1. Solve the MINLP problem as a NLP with all the integer variables relaxed as continuous variables between their bounds.

2. Create the master MIP problem by removing all nonlinear constraints. Construct linearizations around the optimal solution of the NLP (solved in step 1) and add the resulting linear constraints to the master MIP problem.

3. Solve the master MIP problem using a branch-and-bound solver.

4. Whenever the branch-and-bound solver finds a new incumbent solution do:

   1. Solve the NLP problem by fixing the integer variables to the values in the incumbent solution.

   2. Add linearizations around the optimal NLP solution as lazy constraints to the master MIP problem.

   3. Continue branch-and-bound enumeration.

5. Terminate MIP solver if the optimality gap is sufficiently small.

Linearizations are linear outer approximations of the feasible set of the MINLP problem. They are constructed by using the gradient of each nonlinear function in the NLP problem for a certain (optimal) solution to the NLP problem.

In the latest version of COA, which is available in AIMMS 3.13, step 4 is implemented using the lazy constraint callback functionality of a MIP solver. Currently, CPLEX and Gurobi are the only MIP solvers available in AIMMS that support the lazy constraint callback.

Lazy constraints are constraints that represent one part of the model; without them the model would be incomplete. In our case the set of constraints representing a linearization of the nonlinear constraints form the lazy constraints. There are infinitely many of those constraints and therefore it is impossible to add them beforehand to the master MIP problem.

The lazy constraint callback used for step 4 is called whenever the MIP solver finds an integer feasible solution. The callback then either accepts the solution as a solution of the original MINLP problem, or creates one or more lazy constraints (i.e., linearizations) that are violated by the solution.

The previous version of COA, as used in AIMMS 3.9 – 3.12, did not use the lazy constraint callback because it was not available in CPLEX and Gurobi at that time. Instead it used four callbacks, namely the incumbent, cut, heuristic and branch callback functions of CPLEX; Gurobi could not be used because it did not support all of these four callback functions. The new implementation has several advantages:

• A cleaner and easier implementation; using less “tricks”.

• It can also be used for problems with general integer variables.

• It can be used by CPLEX and Gurobi.

• Improved performance.

The old implementation could only be used for problems with binary variables because the branch callback does not allow adding new variables to the existing problem which would be needed when solving a problem with general integer variables.

Using AOA and COA

AOA and COA are not solvers but algorithms that are programmed in the AIMMS Language using GMP functions. To use one of the algorithms you first have to install the system module GMPOuterApproximation. The AOA algorithm is implemented in the AOA Basic Algorithm section of this module and the COA algorithm in the AOA Convex Algorithm section.

Next you have to create an element parameter in your AIMMS project, say, myGMP with range AllGeneratedMathematicalPrograms. To solve a mathematical program myMP that models a convex MINLP problem with AOA you should then call:

myGMP := GMP::Instance::Generate( myMP ) ;
GMPOuterApprox::IsConvex := 1;
GMPOuterApprox::DoOuterApproximation( myGMP );

where GMPOuterApprox is the prefix of the GMPOuterApproximation module. Note that the user has to tell AIMMS that the problem is convex; AIMMS cannot detect whether a problem is convex. To use COA you should call:

myGMP := GMP::Instance::Generate( myMP ) ;
GMPOuterApprox:: DoConvexOuterApproximation( myGMP );

From AIMMS 3.13 onwards COA by default calls the nonlinear presolver of AIMMS [9]. The presolver can reduce the size of a problem and tighten the variable bounds which likely improve the performance of COA. Furthermore, the presolver can often quickly detect inconsistencies in an infeasible problem. Note that the presolver cannot detect inconsistencies for all infeasible problems.

Both AOA and COA can print out a status file that displays progress information, e.g., the objective value, as the algorithm solves the MINLP problem. To print out the status file you should add the following statement:

GMPOuterApprox::CreateStatusFile := 1;

The status file will be printed as the file gmp_oa.put in the log subdirectory. The status file is especially useful in case AOA or COA seems to experience difficulties when solving your problem.

Fig. 23 shows an example of the status file output by COA. A ‘*’ in front of a line indicates that a new best integer solution for the MINLP problem has been found. In this example the algorithm finds its first integer solution with objective value 871267.5847 at the root node of the branch-and-bound tree, a better one with objective value 797830.1734 at node 30 and continuous until it finds the optimal solution with objective value 769440.4204 at node 1251. Thereafter, the algorithm continuous to proof that the final solution is optimal.

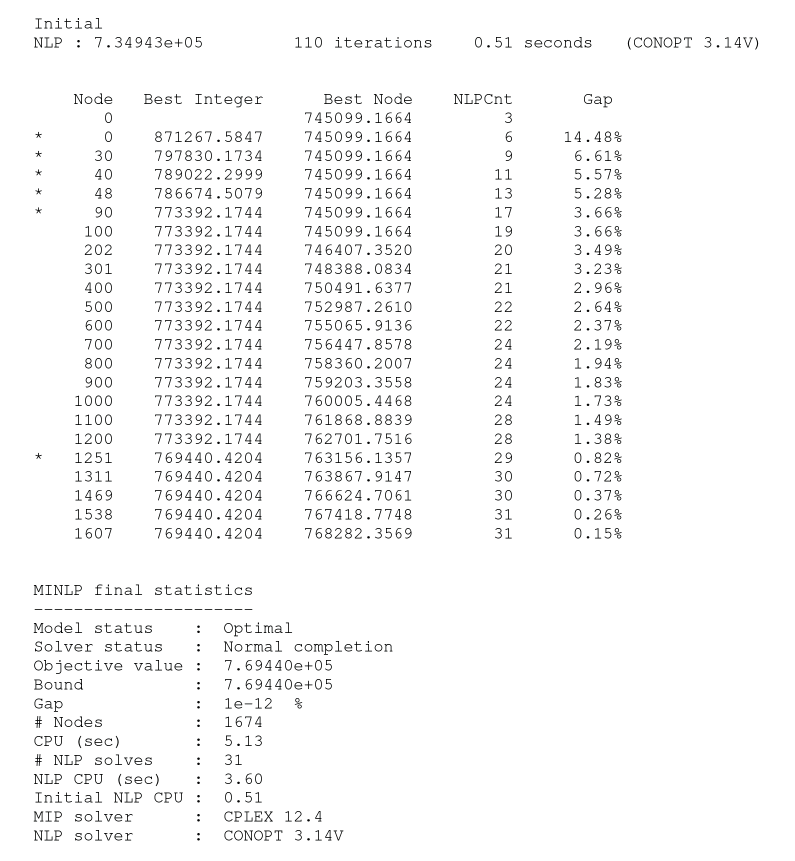
Fig. 23 Example of COA status file output (minimization problem).

Computational Study

To compare the performance of COA with AOA we used test instances from several libraries that are publicly available: the GAMS MINLPLib World [4], the MacMINLP collection [11], the CMU-IBM Cyber-Infrastructure for MINLP collaborative site [6], and the CMU-IBM Open source MINLP Project [7]. A large selection of these instances was used to benchmark other MINLP solvers, e.g., BONMIN [3] and FilMINT [1], but not the instances adata3 and M_SPO_RL from [6]. All these test instances were written for the modeling languages AMPL or GAMS and converted to AIMMS models.

The machines used in the test is a Dell Precision T1500 with an Intel(R) Core(TM) i7 2.80GHz CPU, 12 gigabytes of RAM and running Windows 7. The MIP solver used was CPLEX version 12.4 and the NLP solver was CONOPT version 3.14V.

We used a thread limit of one for CPLEX although the machine we used contains 4 cores. The reason for this is that the results with COA become non-deterministic if callback procedures are installed (as in COA) because then CPLEX might use a different solution path (with a different level of performance) if the same problem is solved again. We used a time limit of 1 hour. We only measure the time used by AOA and COA, excluding the generation time by AIMMS.

Fig. 24 shows the running times of AOA, COA in AIMMS 3.12 (using incumbent, cut, heuristic and branch callbacks) and COA in AIMMS 3.13 (using lazy constraint callback). The problems in Fig. 24 contain no general integer variables. The best running time for each problem is given in bold. The results of Fig. 24 show that COA 3.13 dominates COA 3.12; the few problems for which COA 3.12 is faster the difference in running time is small (except for model fo9 which was solved after 5137 seconds by COA 3.13) but for several problem classes (RSyn, SLay and Water) COA 3.13 clearly performs better than COA 3.12.

For the problem classes Batch, CLay, FLay and SLay, and the problem trimloss4, COA performs better than AOA. For the other problem classes there is no clear winner. AOA and COA 3.13 perform much better than COA 3.12 on the Water problems. This is partially caused by the preprocessing step done by AOA and COA 3.13, and which was not implemented for COA 3.12. Fig. 25 shows the results of AOA and COA 3.13 on the Water problems if preprocessing is switched off. For all the other problems preprocessing did not have a significant influence on the running time.

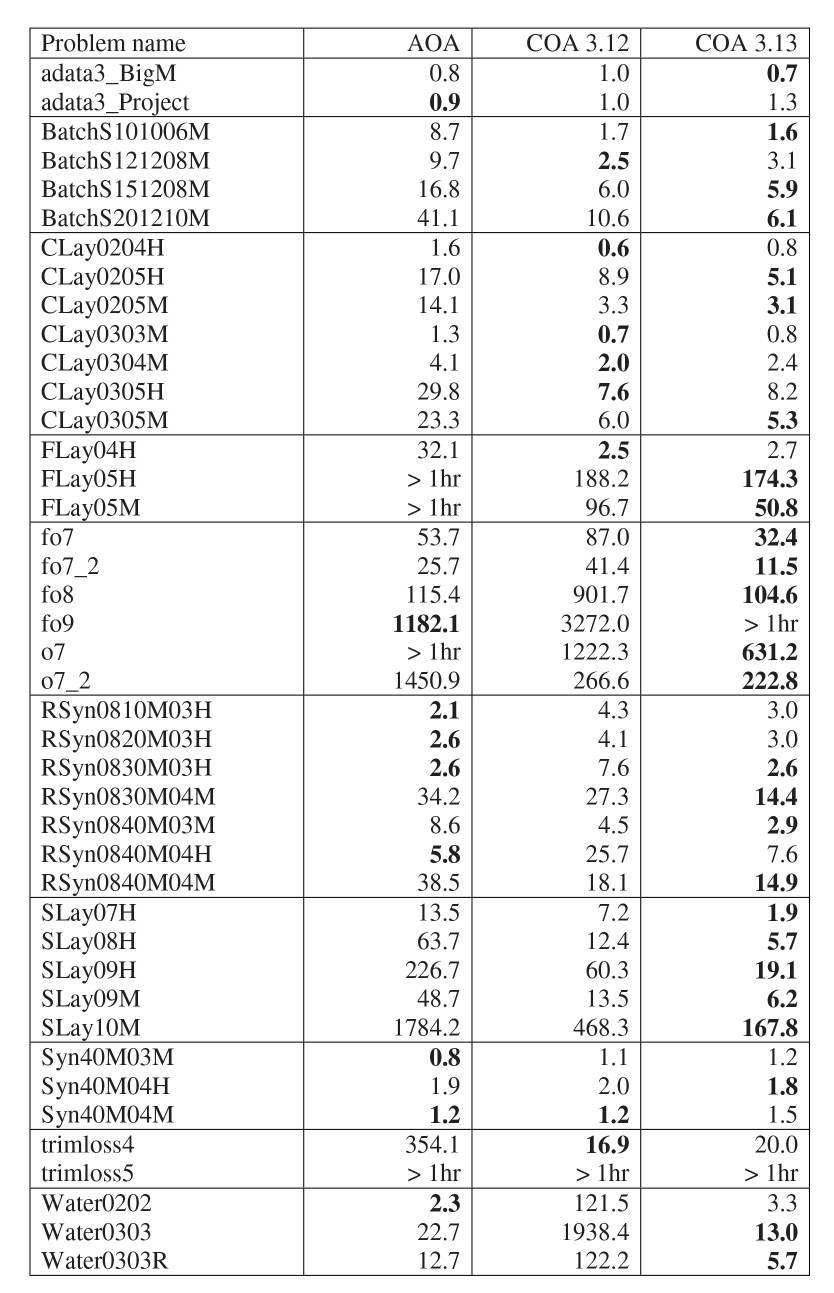
Fig. 24 Running times (in seconds) for problems with binary variables.

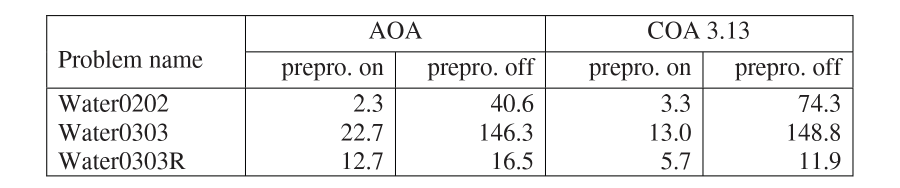
Fig. 25 Effect of preprocessing on running times (in seconds) for Water problems.

Fig. 26 shows results for problems with general integer variables using AOA and COA 3.13. As mentioned before, these kinds of problems cannot be solved using COA 3.12.

Fig. 26 Running times (in seconds) for problems with general integer variables.

Conclusions

AIMMS implements two versions of the outer approximation algorithm, namely the classic version by Duran and Grossmann (AOA) and the one-MIP-tree-search version by Quesada and Grossmann (COA). Computational experiments show that overall COA outperforms AOA.

References

[1] Abhishek, K., S. Leyffer, J. Linderoth, FilMINT: And Outer Approximation-Based Solver for Convex Mixed-Integer Nonlinear Programs, INFORMS Jounrnal on Computing 22(4) (2010), pp. 555-567.

[2] Bisschop, J., M. Roelofs, AIMMS Language Reference, Version 3.12, Paragon Decision Technology, Haarlem, 2011.

[3] Bonami, P., A. Wächter, L.T. Biegler, A.R. Conn, G. Cornuéjols, I.E. Grossmann, C.D. Laird, J. Lee, A. Lodi, F. Margot and N. Sawaya. An algorithmic framework for convex mixed integer nonlinear programs. Discrete Optimization 5 (2008), pp. 186-204.

[4] Bussieck, M.R., A. S. Drud, and A. Meeraus, MINLPLib – a collection of test models for mixed-integer nonlinear programming, INFORMS Journal on Computing, 15 (2003). [Internet: https://www.minlplib.org/].

[5] Byrd, R.H., J. Nocedal, R.A. Waltz, KNITRO: An Integrated Package for Nonlinear Optimization, in: Large-Scale Nonlinear Optimization, G. di Pillo and M. Roma (eds), Springer-Verlag, 2006, pp. 35-59.

[6] CMU-IBM Cyber-Infrastructure for MINLP collaborative site. [Internet: https://www.minlp.org/].

[7] CMU-IBM Open source MINLP Project. [Internet: http://egon.cheme.cmu.edu/ibm/page.htm].

[8] Duran, M.A., I.E. Grossmann, An outer-approximation algorithm for a class of mixed-integer nonlinear programs, Mathematical Programming 36 (1986), pp. 307-339.

[9] Hunting, M., A nonlinear presolve algorithm in AIMMS, An AIMMS white paper, Paragon Decision Technology BV, 2011.

[10] Hunting, M., The AIMMS Outer Approximation Algorithm for MINLP (using GMP functionality), An AIMMS white paper, Paragon Decision Technology BV, 2011.

[11] Leyffer, S., MacMINLP: Test problems for mixed integer nonlinear programming, 2003. [Internet: https://wiki.mcs.anl.gov/leyffer/index.php/MacMINLP].

[12] Quesada, I., I.E. Grossmann, An LP/NLP Based Branch and Bound Algorithm for Convex MINLP Optimization Problems, Computers and Chemical Engineering 16 (1992), pp. 937-947.

[13] Tawarmalani, M., N.V. Sahinidis, Global optimization of mixed-integer nonlinear programs: A theoretical and computational study, Mathematical Programming 99(3) (2004), pp. 563-591.

[14] Viswanathan, J., I.E. Grossmann, A combined penalty function and outer-approximation method for MINLP optimization, Computers and Chemical Engineering 14 (1990), pp. 769-778.