Miller-Tucker-Zemlin formulation

The Capacitated Vehicle Routing Problem Library contains four different formulation options. Those formulations use different methods for eliminating subtours. In this article, the Miller-Tucker-Zemlin formulation is discussed. Herein below an example of a subtour within a route for a CVRP:

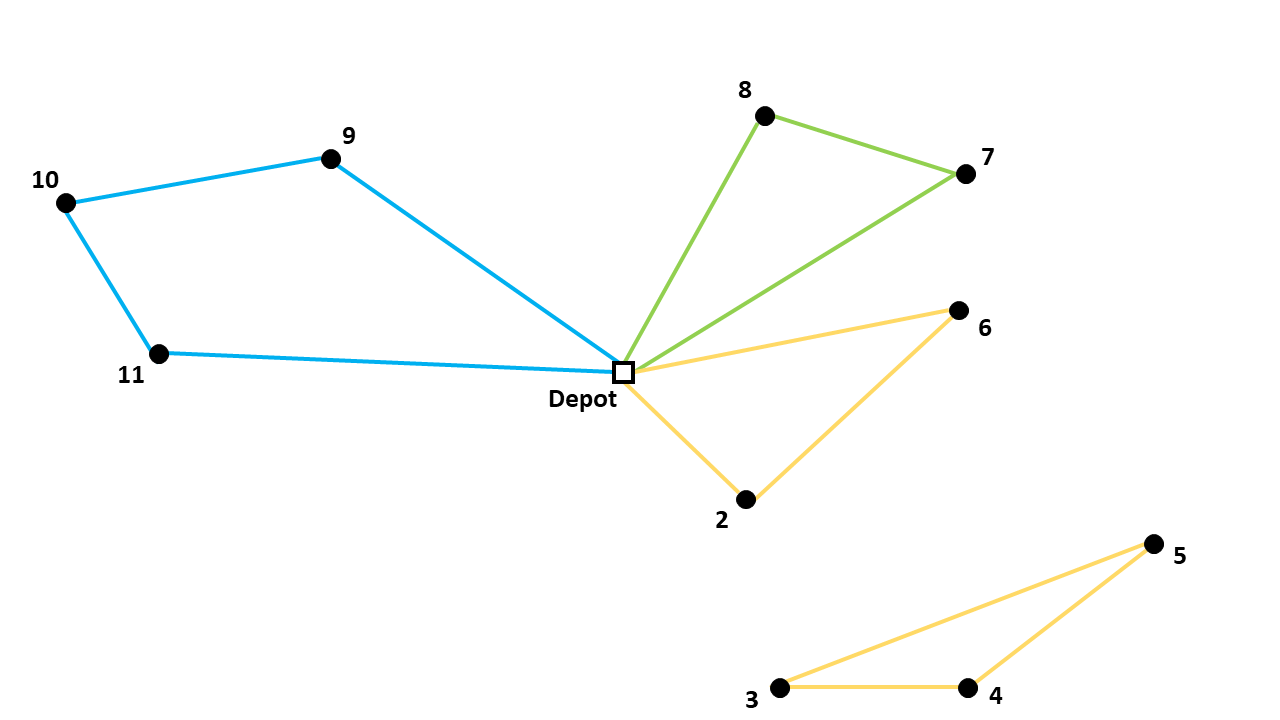
../../_images/Subtour.png

Idea behind the formulation

The Miller-Tucker-Zemlin (MTZ) formulation uses an extra variable. The variable is called \(u_{i}\) and gets a value for each node, except for the depot. If a vehicle drives from node i to node j, the value of \(u_{j}\) has to be bigger than the value of \(u_{i}\).

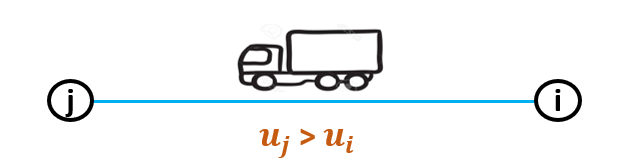
../../_images/MTZ1.png

So each time a new node is being visited, the value for \(u_{i}\) increases.

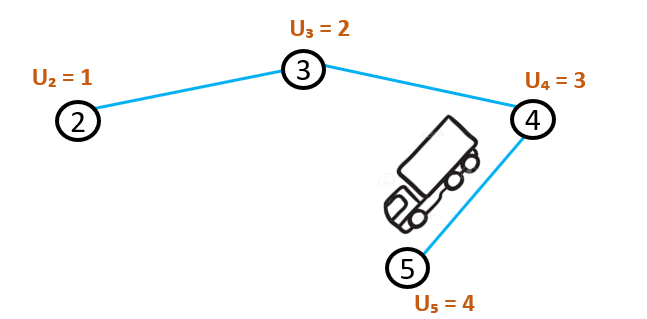
../../_images/MTZ2.png

The node that the vehicle will visit after node 5, should again have a larger value of \(u_{i}\). It would not be possible to go from node 5 to node 2, because that node already has a lower value of \(u_{i}\). This ensures that a vehicle will not drive in a circle. Since that would make it impossible for every value of \(u_{i}\) to be larger than the previous one. Since the depot does not get a value of \(u_{i}\), it is possible to drive in a circle if the vehicle starts and ends at the depot.

../../_images/MTZ3.png

The vehicle can now drive from node 5 back to the depot and \(u_{j}\) is always larger than \(u_{i}\). So the only circles permitted to be driven are the ones passing the depot. All the other circles would be subtours and are eliminated by this formulation.

Subtour Elimination Constraints

The binary variable \(x_{ijk}\) has a value of 1 if vehicle k drives from node i to node j. \(Q\) is the capacity of the vehicles and \(q_{i}\) is the demand of node i. \(V\) is a set containing all the nodes, and the depot is n=1. The constraints can be formulated as follows:

\[u_{j} - u_{i} \geq q_{j} - Q (1 - x_{ijk}) \qquad \forall i,j \in V \setminus \{1\} \enspace i \neq j \qquad (1)\]
\[\qquad \qquad q_{i} \leq u_{i} \leq Q \qquad \forall i \in V \setminus \{1\} \qquad \qquad \qquad (2)\]

If vehicle k drives from node i to node j, \(x_{ijk}\) = 0 and constraint (1) can be rewritten to \(u_{j} \geq u_{i} + q_{j}\). This ensure that the value of \(u_{j}\) is at least \(q_j\) more than \(u_i\). So the value of \(u_j\) is greater than the value of \(u_i\)

If vehicle k does not drive from node i to node j, the constraint is still valid. Constraint (1) could then be rewritten to \(u_{j} - q_{j} \geq u_i - Q\). Constraint (2) states that \(q_j\) is the lowest possible value of \(u_j\) and \(Q\) is the greatest possible value of \(u_i\). So \(u_j-q_j\) will at least be 0 and \(u_i-Q\) will at most be 0. So \(u_j-q_j\) is greater than or equal to \(u_i-Q\)

In the Capacitated Vehicle Routing Problem Library, the constraints are implemented in the section Miller Tucker Zemlin Section.