Model Category Mapping of Items

Very often, you will find yourselves having to define a certain property for an item based on its category. For example, Cost ($) of an item based on the size of that item (small, medium, or large). This is similar to using a lookup function in Excel to create a map from the size-cost table to the list of items. This article will show you how to model such a category mapping in AIMMS.

Please use the following project to follow this article:

Category Modelling Example AIMMS Project

Use Case

A simple example case is if you have a list of different orders for an item (of three different sizes), you know the price per unit for each size and you want to calculate the cost of each order.

s_sizes	p_def_price
Small	3
Medium	5
Large	7

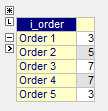
The accurate mapping from the above table to the below table should be 3, 5, 7, 7, 3. How do you lookup the corresponding price for each s_orders according to the ep_def_orderSize?

s_orders	ep_def_orderSize	p_def_orderCost
Order 1	Small
Order 2	Medium
Order 3	Large
Order 4	Large
Order 5	Small

AIMMS Implementation

One way to do this is to define ep_def_orderSize as an element parameter which lets us assign a set element to an indexed parameter.

Important

A parameter type identifier is used to store numerical values, an element parameter type identifier is used to store elements of a set, and a string parameter type identifier is used to store string values like the name suggests. Remember to use an element parameter even if your set contains numerical elements.

In the AIMMS project, you have sets s_sizes and s_orders with i_size and i_order as indices respectively. Price per size is stored in the indexed parameter p_def_price(s).

Order size for each order is stored in an element parameter ep_def_orderSize(i_order) which has the attribute Range defined as as s_sizes. The Range attribute is mandatory for an element parameter and it should be defined as the set which contains the elements to be stored in that element parameter.

Option 1

Now, the cost of each order p_def_orderCost(i_order) can be calculated using the following definition:

Parameter p_def_orderCost_OPTION1 {
   IndexDomain: i_order;
   Definition: p_def_price(ep_def_orderSize(i_order));
}

For each i_order, the corresponding i_size is mapped using the element parameter ep_def_orderSize(i_order). For example, the evaluation of p_def_orderCost_OPTION1('Order 1') will be as follows:

! starting with
p_def_price(ep_def_orderSize('Order 1'))

! will be
p_def_price('Small')

! then
3

Option 2

p_def_orderCost(i_order) can also be computed by defining a binary parameter such as p_def_relationSizeOrder(i_size,i_order), see:

Parameter p_def_relationSizeOrder {
   IndexDomain: (i_size,i_order);
   Range: binary;
   Definition: 1 $ (ep_def_orderSize(i_order) = i_size);
}

And since there is only one size per order, p_def_orderCost_OPTION2(i_order) can be defined as:

Parameter p_def_orderCost_OPTION2 {
   IndexDomain: i_order;
   Definition: {
      sum(i_size |
               p_def_relationSizeOrder(i_size, i_order),
            p_def_price(i_size))
   }
}

Result

The resulting data page of the parameter p_def_orderCost_OPTION1(i_order) or p_def_orderCost_OPTION2(i_order) will look as below: