Optimize Scheduling for Project Planning

The identifier types ACTIVITIES and RESOURCES, and the scheduling intrinsic functions as part of the AIMMS constraint programming component are very useful in modeling construction projects and optimizing the makespan of those projects.

Several existing constraint programming languages use the Bridge Building example in the Ph.D Thesis of the late M. Bartusch to illustrate this, see for instance SAS.

In such a construction project, there are construction activities related to each element of a structure, such as pillars, and to the activities to manage the project itself such as delivery of materials and the building of housing to shelter the construction equipment.

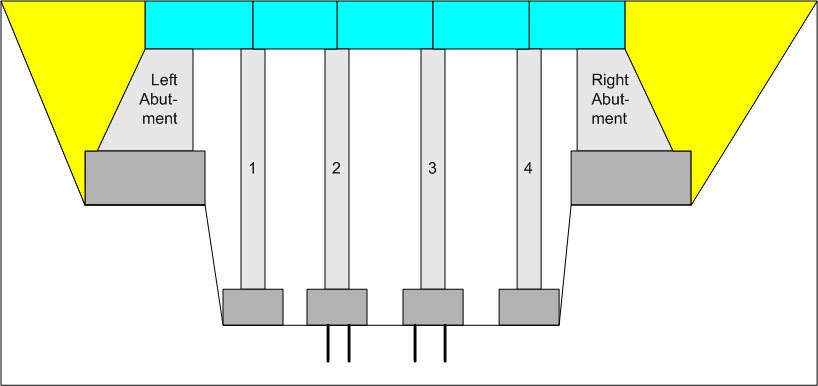
Fig. 34 Bridge Building

A bridge consists of two abutments, several pillars in between, and bearers upon those pillars and abutments. Erecting a pillar requires several steps: excavation, pile driving (if needed), form work, concrete filling and setting, and masonry work. For an abutment, the sand filling is an additional step. A construction step is modeled as:

Activity v_PillarActivity {
    IndexDomain: (epbs,ep);
    ScheduleDomain: cal_TimeLine;
    Length: p_PillarDuration(epbs, ep);
}

Ensuring that two building steps pbs1 and pbs2 are taken in the correct order during the building of a pillar p is modeled in the following constraint:

Constraint c_pillarBuildingOrder {
    IndexDomain: {
        (i_pbs1, i_pbs2, i_p) | p_PillarDuration(i_pbs1,i_p)          and
                          p_PillarDuration(i_pbs2,i_p)          and
                          i_pbs1 < i_pbs2                  /*   and
                          ( not exists( pbs3 | pbs1 < pbs3 and pbs3 < pbs2 and PillarDuration(pbs3,p) ) ) */
    }
    Definition: cp::EndBeforeBegin(v_PillarActivity(i_pbs1,i_p),v_PillarActivity(i_pbs2,i_p));
}

Perhaps interesting is the last condition in the index domain: ( not exists( pbs3 | pbs1 < pbs3 and pbs3 < pbs2 and PillarDuration(pbs3,p) ) ). This condition states that we do not want to incorporate those individual restrictions that can be derived from two other individual restrictions; if the activity PillarActivity(pbs1,p) already takes place before activity PillarActivity(pbs3,p) and activity PillarActivity(pbs3,p) already takes places before PillarActivity(pbs2,p); then this implies that activity PillarActivity(pbs1,p) takes places before activity PillarActivity(pbs2,p) and we do not have to enforce this explicitly. Adding this condition reduces the number of rows from 161 to 86 and improves the number of branches investigated per second by CP Optimizer by roughly 15%.

Each building step i_pbs requires a corresponding resource, and of each resource we have only one. This can be modeled using the following sequential resource:

Resource c_mach_seq {
    Usage: sequential;
    IndexDomain: i_mn | forall( i_mnp, p_NoAvailableMachines(i_mnp) = 1 );
    ScheduleDomain: cal_TimeLine;
    Activities: v_PillarActivity(i_pbs, i_p): (ep_requiredMachineForBuildingStep(i_pbs)=i_mn) and p_PillarDuration(i_pbs, i_p);
}

Having multiple machines of a certain type, we can generalize this to:

Resource c_mach_par {
    Usage: parallel;
    IndexDomain: i_mn | exists( i_mnp | p_NoAvailableMachines(i_mnp) <> 1 );
    ScheduleDomain: cal_TimeLine;
    Activities: v_PillarActivity(i_pbs, i_p): (ep_requiredMachineForBuildingStep(i_pbs)=i_mn) and p_PillarDuration(i_pbs, i_p);
    LevelRange: {
        {0..p_NoAvailableMachines(i_mn)}
    }
    LevelChange: {
        v_PillarActivity(i_pbs, i_p) : 1 $ ( (ep_requiredMachineForBuildingStep(i_pbs)=i_mn)  and p_PillarDuration(i_pbs, i_p) );
    }
}

The entire example can be downloaded from: AIMMS project download

Note

If you are using AIMMS 4.70 or later with this example, you will need to replace .boolean-value-editor input with .boolean-cell-editor-contents in the CSS file .\BuildBridge\MainProject\WebUI\resources\css\scalar-binary-switch.css.

Reference

Bartusch, M. (1983), Optimierung von Netzplänen mit Anordnungsbeziehungen bei knappen Betriebsmitteln, Ph.D. thesis, Universität Passau, Fakultät für Mathematik und Informatik.