Select Constraints and Variables for a Math Program Declaration
In this article we will explore how you can control the constraints or variables used in a math program. Then we’ll show an example of how to use this method to analyze infeasibility of a mathematical program.
A sample declaration of a math program is shown below.
MathematicalProgram Sample_Math_Program {
Objective: ObjFunc;
Direction: minimize;
Constraints: AllConstraints;
Variables: AllVariables;
Type: Automatic;
}
Objectivespecifies which variable is the objective function of the math program.Directionspecifies whether you want to minimize or maximize the objective function.Constraintsspecifies which set of constraints should be considered. In this case,AllConstraintswill be considered.Variablesspecifies which set of variables should be considered. In this case,AllVariableswill be considered.Typespecifies what kind of a problem the math program is, e.g., a linear program, an integer program, and so on. The default optionAutomaticsuffices in most cases and is recommended.
Note
AllConstraints and AllVariables are Model related predeclared identifier Sets, containing all constraints and all variables defined in your model.
You may have multiple mathematical program identifiers in the same project, subject to different sets of constraints and variables. For example, it can be used in a sequential goal programming problem where the solution of the first problem is provided as input to the second problem.
Default Constraints and Variables
When you solve a mathematical program (or generate it via the GMP functions), AIMMS will use the values of the Constraints and Variables attributes of the mathematical program identifier to determine which symbolic variables and constraints should actually be considered in the model.
The default values of Constraints and Variables attributes are the predefined sets AllConstraints and AllVariables respectively. AllConstraints contains all the constraints declared in your AIMMS project and similarly, AllVariables contains all the variables.
Variables with definition
For variables with a definition, AIMMS will actually generate both the variable and an additional equality constraint. For example, if you have the variable X that has Y + Z in its definition attribute:
Variable X {
Range: free;
Definition: Y+Z;
}
AIMMS will generate:
Variable
XEquality constraint
X_definitionasX = Y + Z
So, any variable with a definition (like X) will appear in both the predeclared sets AllConstraints and AllVariables.
Selecting Constraints or Variables
To select the constraints to be applied in a math program, you can create a set as a subset of AllConstraints and use that set in the declaration of the math program instead of AllConstraints.
Likewise, you can create a subset of AllVariables and use it in the declaration of the math program.
The below below example shows two sets, ModelConstraints and ModelVariables, used in the math program Sample_Math_Program.
Set ModelConstraints {
SubsetOf: AllConstraints;
Definition: AllConstraints*Section_or_Declaration_to_Optimize;
}
Set ModelVariables {
SubsetOf: AllVariables;
Definition: AllVariables*Section_or_Declaration_to_Optimize;
}
MathematicalProgram Sample_Math_Program {
Objective: ObjFunc;
Direction: maximize;
Constraints: ModelConstraints;
Variables: ModelVariables;
Type: Automatic;
}
You can either manually select the constraints and variables to be included in these subsets or use the definition, as shown above, to include all the constraints and variables present in a particular section or declaration section.
Using a definition makes it easy to scale the project — any new constraint or variable added inside Section_or_Declaration_to_Optimize is automatically added to the subset and used in generating the math program. You do not need to select variables with a definition in both the subsets.
Analyzing infeasibility of a mathematical program
Using the above method can be used to a quick analysis on the infeasibility of a mathematical program.
We’ll use an example project, which you can download from the link below:
Run
MainExecution. The Progress Window shows “Model infeasible” and there is a warning in the error/warning window.
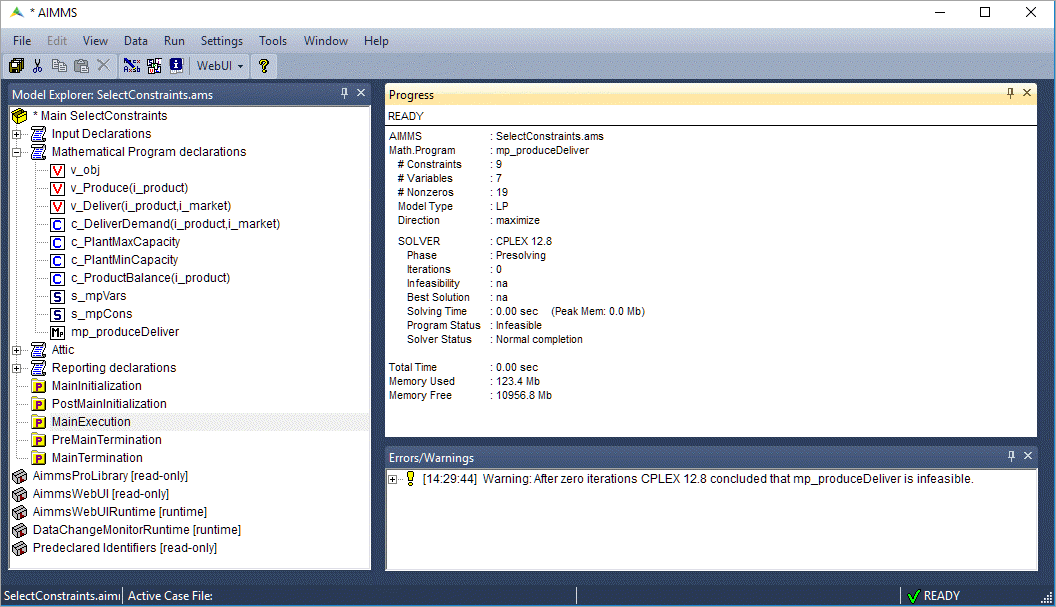
Move the declaration of the constraint
c_PlantMinCapacityto the declaration section “Attic” (that famous place where you put stuff you don’t use, but don’t want to throw away).

Run
MainExecutionagain. The Progress Window now shows “Model feasible”.
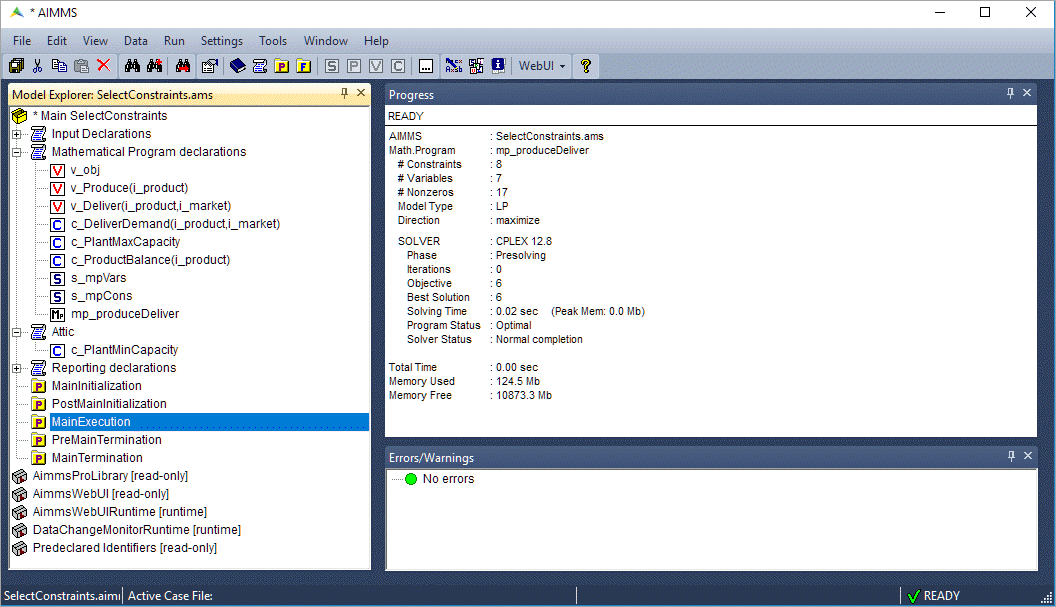
Under the hood, the set s_mpCons is recomputed removing the constraint c_PlantMinCapacity from the mathematical program.