Use a Multi-Objective Approach

In this article we will compare a multi-objective approach to separately solving single objectives.

Let’s take for an example a problem trying to find a healthy diet for a reasonable price. First let’s define our objectives:

• minimize calories: I’m trying to lose some weight, so my healthy diet should be low in calories.

• minimize price: a reasonable price means that it doesn’t have to be the absolute minimum, but should be within a close range.

Of course, I want to include minimum/maximum requirements for nutrients such as proteins. Please use the following project to follow this article:

DietProblem.zip

Multi-Objective Approach

Let’s use the multi-objective feature available since AIMMS 4.65 and CPLEX 12.9.

Procedure SolveMultiObj {
    Body: {
        ep_GMP := gmp::Instance::Generate( DietProblem );

        p_retcode := GMP::Column::SetAsMultiObjective(
            GMP      :  ep_GMP,
            column   :  TotalCost,
            priority :  2,
            weight   :  1,
            abstol   :  0,
            reltol   :  0.1);
        if not p_retcode then raise error "Unable to set TotalCost as an objective" ; endif ;

        p_retcode := GMP::Column::SetAsMultiObjective(
            GMP      :  ep_GMP,
            column   :  TotalCalories,
            priority :  1,
            weight   :  1,
            abstol   :  0,
            reltol   :  0.0);
        if not p_retcode then raise error "Unable to set TotalCalories as an objective" ; endif ;

        GMP::Instance::Solve( ep_GMP );
    }
}

There are several remarks on the above:

1. Because the TotalCost objective has a higher priority value, it will be solved first.

2. Because the reltol argument on line 11 has value 0.1, subsequent solves will not increase the total cost by more than 10%.

Single Objective Approach

To be able to compare the multi-objective procedure to traditional single objective solves, there are also two solution procedures in this application:

1. MainExecution, a traditional single objective solve minimizing total cost.

2. SolveMinCalo, a traditional single objective solve minimizing total calories.

Comparing Results

The application has both WinUI and WebUI interfaces, but WebUI is featured in the following screenshots.

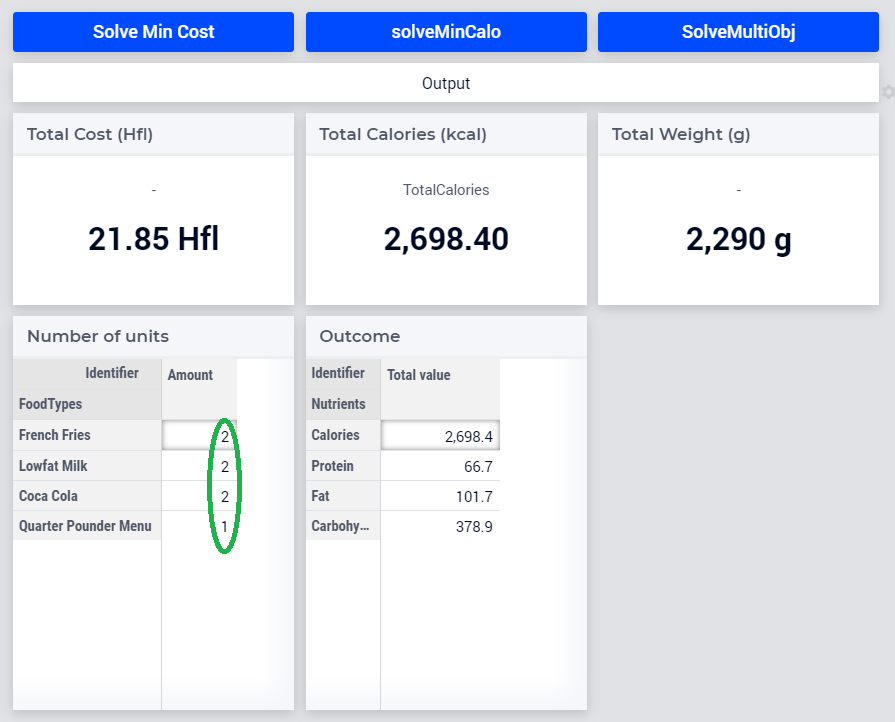
Fig. 20 Results after minimizing total cost

Fig. 21 Results after minimizing total calories

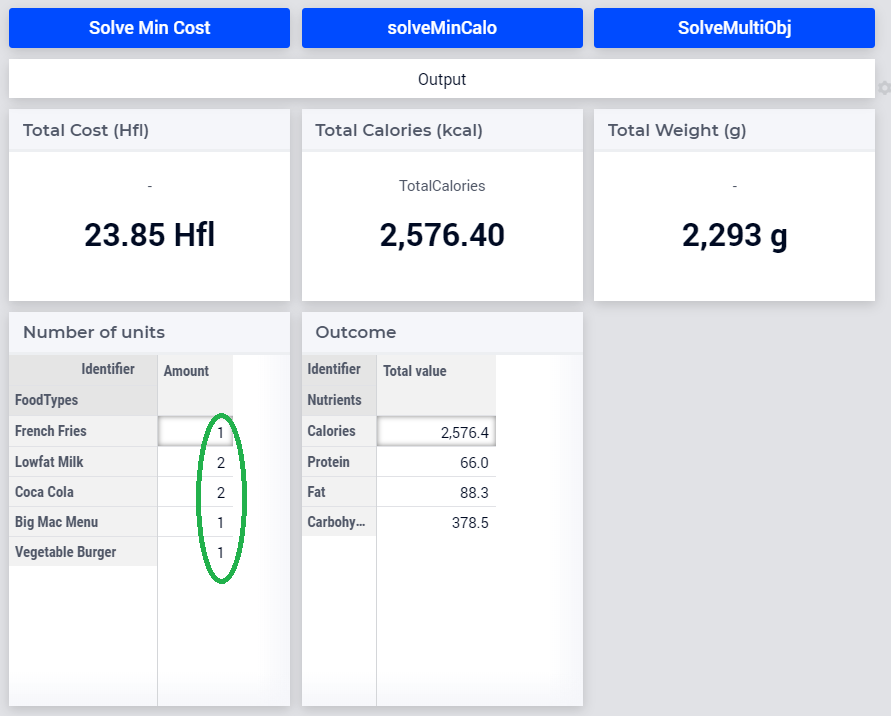
Fig. 22 Results after running multi objective

The objectives are summarized in the table below:

	Cost	Calories
Minimize total cost	21.85	2698.40
Minimize total calories	29.80	2546.40
Multi objective	23.85	2576.40

As you can see, the multi-objective values are not as good as either of the individual objective values, but the multi-objective approach provides a good balance.

You may also find the CPLEX log interesting, as found in the file log/cplex 12.9.sta.

See also

• Retrieve Solver Log Files in AIMMS Developer

Solve problem 'DietProblem' with 9 rows, 15 columns (0 binaries, 9 generals), and 83 nonzeros.

MIP - Integer optimal solution:  Objective = 2.1849999998e+01
Solution time = 0.09 sec.  Iterations = 20  Nodes = 0

Solve problem 'MinCaloDietProblem' with 9 rows, 15 columns (0 binaries, 9 generals), and 83 nonzeros.

MIP - Integer optimal solution:  Objective = 2.5464000000e+03
Solution time = 0.02 sec.  Iterations = 13  Nodes = 0

Solve problem 'DietProblem' with 8 rows, 14 columns (0 binaries, 9 generals), and 73 nonzeros.

Multi-objective solve log . . .

Starting optimization #1 with priority 2.

Finished optimization #1 with priority 2.
Objective =  2.1849999998e+01,  Nodes = 0,  Time = 0.05 sec. (0.45 ticks)
Cumulative statistics:  Nodes = 0,  Time 0.05 sec. (0.45 ticks)

Starting optimization #2 with priority 1.

Finished optimization #2 with priority 1.
Objective =  2.5764000000e+03,  Nodes = 0,  Time = 0.02 sec. (0.43 ticks)
Cumulative statistics:  Nodes = 0,  Time 0.06 sec. (0.89 ticks)

MIP - Multi-objective optimal
Solution time = 0.08 sec.  Iterations = 43  Nodes = 0

A breakdown of above log:

• lines 1 - 4 for the first solve (minimize total cost)

• lines 6 - 9 for the second solve (minimize total calories)

• lines 11 - 28 for the multi objective solve.