Adapt Solve Procedure with Callbacks for GMP
This article presents a general guide to converting from solve statements to using GMP, and how to adapt the existing callbacks and their activation.
As an experienced model builder, you may want to convert from solving using the solve statement to using GMP functionality (with prefix gmp::). Using GMP offers several benefits, such as:
Speed up Monte Carlo analysis
Work with multiple solutions
Use multi-objective, both weighted and lexicographic
Solve in parallel
However, when callbacks are used on the mathematical program, the callback procedures need to be modified and activated differently when using GMP.
Original Solve Procedure
We have a flow shop model that is solved by the following procedure pr_DoSolve with body:
1Empty AllVariables;
2pr_GenerateData();
3empty s_Timepoints ;
4
5FlowShopModel.CallbackTime := 'pr_TimeCallback'; ! Solve style callback.
6
7block where progress_time_interval := 1 ;
8 solve FlowShopModel;
9endblock ;
10
11pr_prepInterface;
On line 5 a callback is activated for the flowshop model by setting the corresponding suffix for the mathematical program.
The callback procedure itself is:
Procedure pr_TimeCallback {
Body: {
pr_updateGap(FlowShopModel.bestbound, FlowShopModel.Incumbent);
}
}
As you can see, it uses the suffixes .bestbound and .Incumbent which are set before this procedure is invoked.
An example solve results in the following progress window:
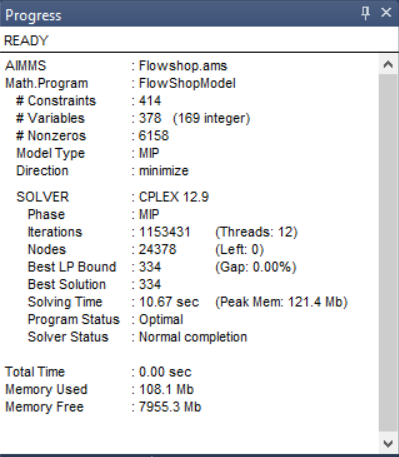
As you can see, optimality is reached.
Example Project 1
If you want to replay this yourself, please download and run 1.flowshop...zip and press the solve button in the lower right corner.
Declaring the GMP
The Generated Mathematical Programs are objects stored in AIMMS internally. Each object is given an identification as an element in the predeclared set AllGeneratedMathematicalPrograms. We use an element parameter to store such an element after generating, so that we can reference it in later manipulations such as solving. The declaration is:
ElementParameter ep_GMP {
Range: AllGeneratedMathematicalPrograms;
}
With this declaration, we can simply convert.
1Empty AllVariables;
2pr_GenerateData();
3empty s_Timepoints ;
4
5FlowShopModel.CallbackTime := 'pr_TimeCallback'; ! Solve style callback.
6
7block where progress_time_interval := 1 ;
8 ep_GMP := gmp::Instance::Generate( FlowShopModel );
9 gmp::Instance::Solve( ep_GMP );
10endblock ;
11
12pr_prepInterface;
The only difference in coding the solution procedure is then on lines 8 and 9, highlighted above. Running that procedure gives the unexpected result:
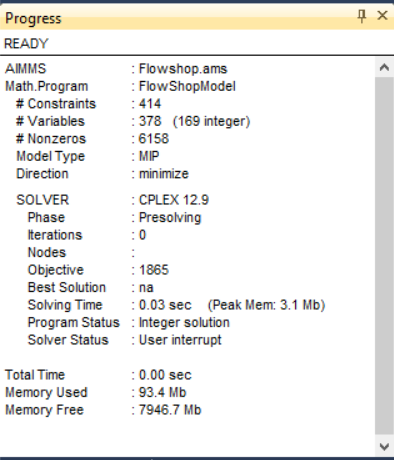
As you can see, optimality is not reached; instead you’ll get the following warning:
After zero iterations CPLEX 12.9 found an integer solution to FlowShopModel. The minimum found for TimeSpan is 1865.
This is caused by the different interface for callbacks. We will handle that in the next section.
Example Project 2
If you want to replay this yourself, please download and run 2.flowshop...zip and press the solve button in the lower right corner.
Adapting Callbacks for GMP
GMP style callback procedures have the input argument ep_session which is an element parameter in the set AllSolverSessions. This gives you access to solver session specific information. The return value of the callback procedure should be 0 to stop solving, or 1 to continue solving.
The best practice is to have an explicit return statement as the last statement of a callback procedure. This results in the following replacement of the pr_TimeCallback procedure.
Procedure pr_TimeCallback {
Arguments: (ep_session);
Body: {
p_BestBound := GMP::SolverSession::GetBestBound( ep_session );
pr_updateGap(p_BestBound, p_BestIncumbent);
return 1 ; ! Indicate to the solver to continue.
}
ElementParameter ep_session {
Range: AllSolverSessions;
Property: Input;
}
Parameter p_BestBound;
}
The solver session allows you to obtain various information from the session directly, but not the incumbent. Instead, we register the latest incumbent value ourselves when the solver finds a new incumbent solution. This requires the following additional procedure:
Procedure pr_IncumbentCallback {
Arguments: (ep_session);
Body: {
p_BestIncumbent := GMP::SolverSession::GetObjective( ep_session );
return 1 ; ! Indicate to the solver to continue.
}
ElementParameter ep_session {
Range: AllSolverSessions;
Property: Input;
}
}
These two callback routines are activated as shown in the following version of the procedure pr_DoSolve:
1Empty AllVariables;
2pr_GenerateData();
3p_BestIncumbent := 1000;
4empty s_Timepoints ;
5block where progress_time_interval := 1 ;
6 ep_GMP := gmp::Instance::Generate( FlowShopModel );
7 gmp::Instance::SetCallbackTime(
8 GMP : ep_GMP,
9 callback : 'pr_TimeCallback');
10 GMP::Instance::SetCallbackNewIncumbent(
11 GMP : ep_GMP,
12 callback : 'pr_IncumbentCallback');
13 gmp::Instance::Solve( ep_GMP );
14endblock ;
15pr_prepInterface;
After running the adapted model, the progress window shows the following results:
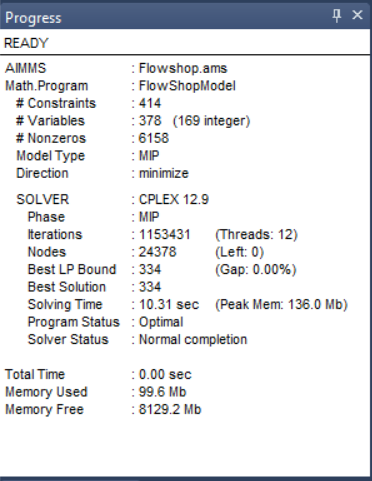
Example Project 3
If you want to replay this yourself, please download and run 3.flowshop...zip and press the solve button in the lower right corner.
You have now converted the Solve statement to use GMP!