Data for Optimization Libaries

An AIMMS library can be reused in other projects. To solve an optimization problem in a library we’re dealing with two abstraction mechanisms:

  • Procedures where sets transferred via the arguments have different meanings.

  • Declare global variables and constraints with a fixed index domain within the library, and use subsets of AllConstraints and AllVariables locally within that library.

These two abstraction mechanisms do not work together naturally.

This article explains how we can bring these two abstraction mechanisms together using element parameters.

The running example

We’ll use an example based on the Transport Problem.

The Transport Problem searches for the best way to transport goods from a couple of sources to sinks.

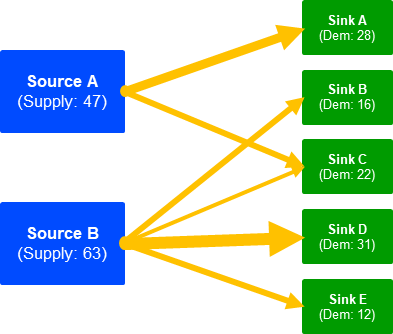
../../_images/TransportProblem.png

AIMMS 4.69 project download

To run this model, load the case Data, and then run procedure MainExecution.

Transferring data

A Transport Problem can be solved locally inside the library.

The following input data is declared in the main model:

  • s_Sources

  • s_Sinks

  • p_Supply

  • p_Demand

  • p_TransportCost

This data must be transferred into the library to solve the problem.

Then, the following output data must be transferred back to the main model: * p_TotalTransportCost * p_Transport

We’ll use the procedure pr_SolveTransportProblem to complete the transfer in two steps (see image):

  1. Provide data from Main Transport to the procedure pr_SolveTransportProblem inside the library.

  2. Transfer data from pr_SolveTransportProblem to the global Declaration of the Transport Library.

../../_images/data.png

These steps are explained in more detail below.

Step 1

Firstly, the procedure pr_SolveTransportProblem should contain local arguments. They can be added by pressing the wizard next to arguments. It is important to select the correct type and property of the arguments. (also something about index)

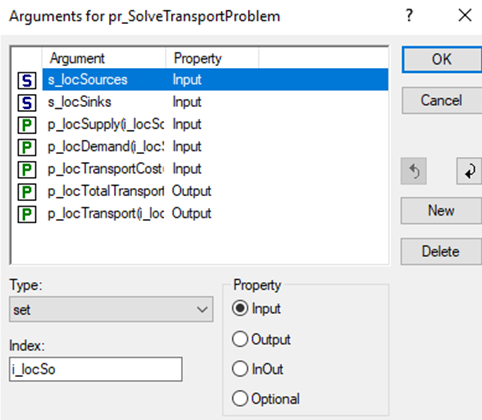
../../_images/Arguments.png

Now we can call the procedure from the main model. We must provide the input and output arguments in the right order to link them to the local arguments.

Call the procedure as follows:

pl::pr_SolveTransportProblem(s_Sources, s_Sinks, p_Supply, p_Demand, p_TransportCost,
p_TotalTransportCost, p_Transport);

Step 2

Next we’ll transfer the data to the global declaration of the library.

In the main model there is a parameter (s_Supply) that describes the supply of the sources (s_Sources). When transferring the data, we must link supplies to the correct sources with element mapping:

1 For i_locSo do
2     SetElementAdd(s_libSources, ep_new1, i_locSo);
3     ep_map1(ep_new1) := i_locSo;
4 EndFor;
5 p_libSupply(i_libSo) := p_locSupply( ep_map1(i_libSo));

  • line 1: i_locSo is the index of s_locSources.

  • line 2: Add the elements to s_libSources.

  • line 3: Map the local sources set the library sources set.

  • line 5: Link supplies to the right sources.

The rest of the input data is transferred in a similar way.

Then the Transport Problem is calculated and the output data is transferred back like this:

p_locTotalTransportCost := v_libTotalTransportCost;
p_locTransport(ep_map1(i_libSo), ep_map2(i_libSi)) :=
    v_libTransport(i_libSo,i_libSi);