Reduce the Time Window for Scheduling Jobs

Scheduling problem

The purpose of this example is to illustrate a few features of the AIMMS identifier types ACTIVITIES and RESOURCES.

In the example used, we model the intuition that smaller jobs get a more narrow time window in which they are to be scheduled. In addition, the time needed between jobs, the change over time, increases with the difference in jobs.

A scheduling problem is a decision problem to schedule jobs respecting restrictions on the resources these jobs use. Scheduling problems represent time as a discrete set, which we call the problem schedule domain. Frequently, the name of this problem schedule domain is ‘Timeline’ as is the case here. In this example we declare ‘Timeline’ as a CALENDAR with time unit a single day.

For the scheduling problem in this example, several jobs are to be executed in sequence without interrupt. A single activity suffices to model the execution of a single job. Each job j has a length: actLen(j), a first possible starting date: StartTime(j), and a deadline: EndTime(j). There is a single worker, which executes only one job at a time. In addition, this worker requires a change over time between two jobs j and k: JobChgOver(j,k).

The objective is to fit the jobs on a single machine within the given time windows, and if possible, to minimize the makespan. The makespan is the end of the last job executed.

In the Three field notation for scheduling problems this problem can be expressed as \(1|r_i ; \bar{d_i} ; s_{ij}|C_{\mathrm{max}}\).

The data of actLen, StartTime, and EndTime is constructed such that the smaller the job, the more narrow the time window is in which this job can be executed. The data of JobChgOver is constructed such that it slowly increases with the difference between jobs. This is illustrated in the following Gantt Chart:

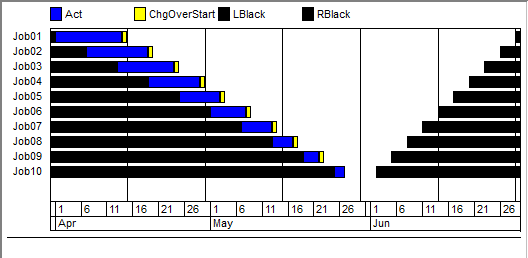
Fig. 33 Gantt Chart Example Narrowing

The part of timeline where a job is not allowed to be scheduled is blacked out. AIMMS will move the blue activities act(j) inside the allowed bounds. Initially, the yellow change over times are just 1 day.

The AIMMS declarations for the involved activities is:

Activity Act {
    IndexDomain: (j);
    ScheduleDomain: {
        {StartTime(j)..EndTime(j)}
    }
    Length: actLen(j);
}

The time window is compactly represented here in the attribute schedule domain of activity ACT. Here StartTime and EndTime are element parameters in the problem schedule domain.

The worker is represented by a single sequential resource:

Resource res {
    Usage: sequential;
    ScheduleDomain: TimeLine;
    Activities: Act(j);
    Transition: (act(j), act(k)) : JobChgOver(j, k);
}

This declaration states that it needs to execute all activities act(j), one at a time, and that there is a change over time between activities.

The complete example is presented in this AIMMS project download

The above Gantt Chart is a screen shot from the demo page. Pressing the solve button on this demo page will show that CP Optimizer is able to find a feasible solution in a fraction of a second. In addition, note that the rows of the Gantt Chart are re-ordered such that the jobs are ordered on their begin time.