Power Systems Planning - Methods and Applications

Warning

This article references outdated technology and is provided for historical purposes only. It is not recommended to use this information as a primary source for current projects or documentation. Please refer to the latest documentation for up-to-date information.

In this document a brief overview of methods and applications of planning in power systems is outlined. Normally, power system planning is required for continuous safe and reliable operation of electricity grids as well as energy networks. In electric power systems, depending on the planning timescale, we can have both long-term planning problems concerning investment in infrastructure and procurement of additional capacity, and short-term planning problems concerning the optimisation of the operation of already existing infrastructure and assets within an electricity network. In this section we only consider short-term planning problems which come in two forms depending on their timescale and required outcome:

1. The Unit Commitment (UC) Problem: which concerns with finding an optimum set of committed generators in the system to maintain the system operational security by ensuring enough generation capacity is available to meet demand within a pre-specified timescale. In mathematical terms, the UC problem is essentially a non-linear mixed integer optimisation problem but normally we solve this as a mixed integer linear programme by ignoring voltage constraints and linearising the objective function.

2. The Optimal Power Flow (OPF) Problem: which concerns with finding an optimum generation schedule of committed generators in the system within a pre-specified timescale. The main difference between the OPF and UC problem is that the OPF only concerns with identifying and optimising (for cost) the generation schedule of already committed generators whereas the UC problem concerns with identifying the committed generators in the first place. Similar to the UC problem, the OPF at its core is a non-linear optimisation problem but we can solve the OPF again by ignoring voltage constraints as a linear programme. There may or may not be integer variables in an OPF problem but that mostly depends on the nature of the problem.

Normally we say that the UC and OPF problems belong to the class of Short Term Optimum Operations Planning problems in power systems planning jargon.

A graphical representation of the various timescales of different power systems planning problems is shown below:

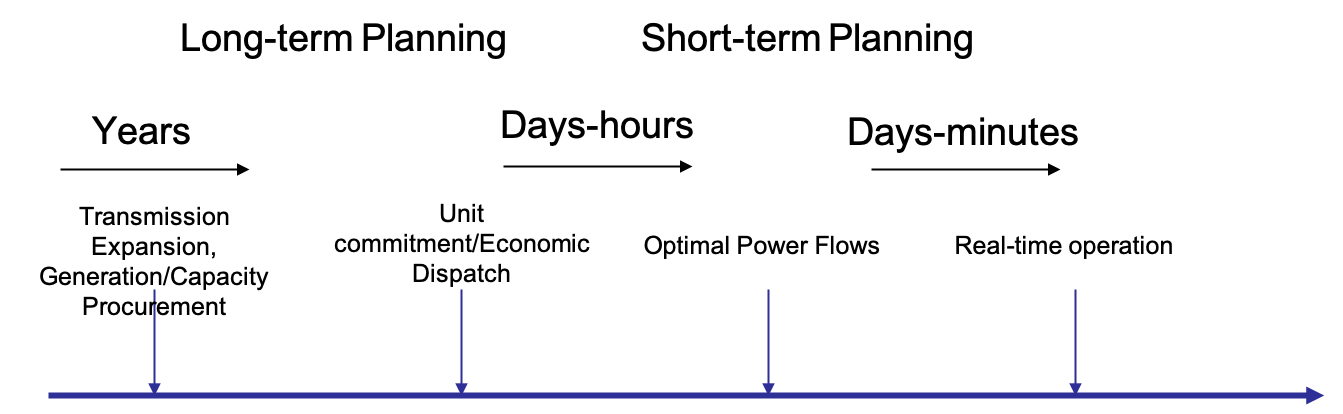
Fig. 71 Figure 1 - Timelines for various Power System Planning Problems

Note

For a more expansive formulation of the power system optimum operations planning problems we suggest reviewing the MATPOWER - MOST User’s Manual

Tutorials

We have included two AIMMS tutorials for formulating and solving the above power system planning problems (UC and OPF). You can navigate the pages below to find the required tutorials:

• Optimal Power Flow (OPF)
  • OPF problem
  • OPF Formulation
  • OPF Implementation in AIMMS
• Unit Commitment
  • Objective Function
  • Constraints
• References

Note

The UC tutorial is currently under construction but you can still use the page above to get an idea of the standard formulation of the UC problem which you can implement in AIMMS.

Acknowlegment

These tutorials were made available thanks to great work of Dr. Bezhad Kazemtabrizi, Dr. Mahmoud Shahbazi and Dr. Abraham Alvarez-Bustos from the Durham University.